Please read the Introduction to Linear Regression before continuing to read this Polynomial Regression article.
Brief summary of regression in Machine Learning (ML) is a type of supervised learning algorithm, it is used for predicting continuous numerical values based on input data. It aims to model the relationship between independent variables (features in training data) and a dependent variable (target of the training data) by fitting a function to the data. The predicted values are continuous, meaning they can take any value within a given range from the trained data.
Examples of regression algorithms include Linear Regression, Polynomial Regression, Decision Tree Regression, etc. Linear regression is the most basic algorithm and easy to understand because it is just a simple math formula to create a linear line to predict output (y) from input (X), the X can be consist of a single value (single feature or 'Simple Linear Regression') or multiple values (multiple features or 'Multiple Linear Regression').
Simple Linear Regression formula is:
y = (X * coefficient) + intercept
Multiple Linear Regression formula is:
y = (X11 * coef1) + (X22 * coef2) + (X33 * coef3) + (Xnn * coefn) + intercept
Polynomial regression is used when the relationship between the independent variable and the dependent variable is not linear, often the real data to be trained cannot be adequately modeled by a straight line (linear). Polynomial regression is a special case of Multiple Linear Regression, one example of formula:
y = (X11 * coef1) + (X22 * coef2) + (X33 * coef3) + (Xnn * coefn) + intercept
Similar to linear regression, due to noise in data and numerical precision, polynomial regression models also cannot predict data with 100% accuracy. Even when predicting the same data from the trained dataset.
Describing the math formula in depth is outside the scope of this article, but we can use graph to help us to visualize and understand how Polynomial Regression can fit better than Linear Regression.
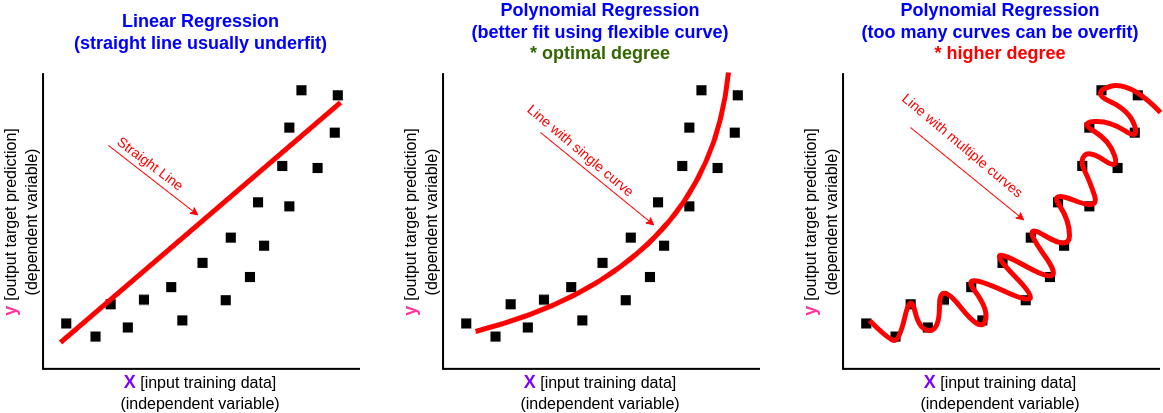
Optimal degree vs higher degree (overfit).
Example case scenarios to use AI prediction using Regression algorithm:
- A single feature based on body weight to predict person shoe size.
- Multiple features based on city (location) and the house size to predict House price.
- Multiple features based on car brand, year (age) and total mileage to predict Used-car price.
- Multiple features based on total year of work experience, Python language skill score, C/C++ language skill score and Javascript skill score to predict software developer salary.
For beginner in machine learning to get better understanding of how Polynomial Regression is better than Linear Regression, these are the steps:
- Get the data to make the model
- Analyze the correlation features of the data, remove uncorrelated features.
- Eg: in house price prediction, the total door and total windows may not have strong correlation therefore these features can be removed.
- Split data for prediction and for testing
- To evaluate the model we should not use data from other source, we only trust all data points from this same source.
- To create unseen data to get performance of the model using unseen data later.
- Find optimal Polynomial degree (prediction trial)
- Polynomial degree parameter is start from 2
- Do multiple trials to build the model and predict
- Check and compare the R2 score to get the highest R2 score
- Predict training data.
- Predict unseen test data.
- Compare performance
- In polynomial regression, it's common for the R-squared (R^2) score and mean absolute error (MAE) to be more favorable on the training data compared to unseen or test data. This phenomenon is known as overfitting.
- If the prediction result of the training data and unseen test data are close (similar) then the model is good.
- If the prediction result is far (a lot of gaps) then the model maybe overfit, need to reduce 'degree' value.
- Extra: Find outlier (data point that is noticeably different from the rest which may be considered as "invalid" data)
- Using Mean Absolute Error (MAE) & Threshold to find outliers.
- If we found outliers then we can do further analysis to
- Check if there is any features that is not a strong correlation to the target value.
eg: in house price prediction, the 'total doors' and 'total windows' may not have strong correlation to the price therefore these features can be removed. - Delete outliers to improve model accuracy.
- Check if there is any features that is not a strong correlation to the target value.
All the steps above can be reviewed in this simple Polynomial Regression demo using Python code in Jupyter Notebook, Github: Polynomial Regression
Some benefits to use Polynomial regression instead of Linear regression:
- Capturing Non-Linear Relationships: Linear regression assumes a linear relationship between variables, but real-world relationships can be more complex. Polynomial regression can capture non-linear patterns in the data, providing a better fit.
- Flexibility: Polynomial regression allows for a more flexible curve to be fitted to the data. By introducing higher-degree polynomial terms, the model can accommodate more complex relationships between variables.
- Improved Accuracy: In situations where the relationship between variables is non-linear, polynomial regression can provide more accurate predictions compared to linear regression.
- Better Model Interpretation: While polynomial regression introduces complexity, it can also provide insights into the curvature and shape of the relationship between variables, which may be valuable for interpretation.
Disadvantages when use polynomial regression instead of linear regression:
- Overfitting: It is very easy to overfit by using higher degree value, the predicted result is more suitable for trained data and not suitable for unseen data.
- More complex: need to put more care to generalize the 'degree' of polynomial terms to fit the data.
- On creating Polynomial Regression, we need to define an integer value of 'degree'.
- In some cases using smaller 'degree' value may be underfit but higher 'degree' value may cause overfit.
- Tip: scikit-learn has a function r2_score() to compare which 'degree' value is optimal fit for the data
* return value of r2_score() is between 0.0 to 1.0 (but a negative value is possible), closer to 1.0 means better and a value of 1.0 means perfect match.